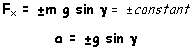Restoring force (horizontal): component of the gravity force depending only on the inclination (±g)

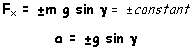
The observed "horizontal oscillation" is due to the horizontal component of the gravity force acting on the center of mass of the sphere which is bound to move on the rail .

The vertical component of the speed changes direction each time the sphere goes through the lowest quote. In the vertical direction the center of mass behaves as a "bouncing ball".

The horizontal component of the motion is isomorph to the Atwood oscillator: also here the restoring force "changes direction" when the body crosses the equilibrium position.

Oscillation is therefore anharmonic

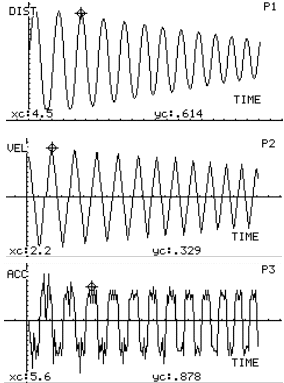
1. The plots x(t), v(t), a(t), f(t) vs. time are similar to those for Atwood oscillator. Motion is indeed uniformly accelerated.
2. The restoring force is F= -mg sinf sgn(x) , and therefore it depends on the tilt f.
3. The measured acceleration (slopes in v(t) or mean values on a(t) plots) may be compared with the value predicted by the model: it will come out that the sphere moment of inertia must be taken into account. Using a ping-pong ball (instead of an homogeneous sphere) demonstrates the role of mass distribution in rotational dynamics.
4. The agreement between theoretical prediction and experimental values may be not satisfactory. By repeating the experiment with the same sphere and a larger rail the disagreement increases, (as well as using the same rail and a smaller sphere). The teacher may ask the students to try explaining the reason why (effect of a giration radius different from sphere radius).


CONTINUE ...