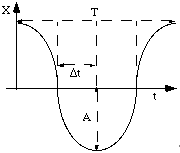
x(t) plot made of a series of parabolas corresponding to "fall" from height A upward (in water) and downward (in air).
 
 

Predicted period : 

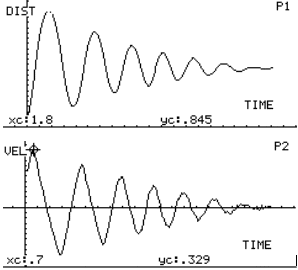
1. The plot x(t), vs. time looks like the corresponding one for the mass-spring oscillation, and this could suggest an harmonic behavior.
2. However the plots v(t) and a(t) demonstrate that this motion resembles that of a bouncing ball, of the cart on the incline and yo-yo: it is a uniformly accelerated motion during most part of the time. It can be studied following the same analysis.
3. In the case of small oscillations (with the cylinder always partially immersed) the motion turns into a damped harmonic motion .
4. By performing a full set of measurements of the period T and by studying the plot of T vs. sqrt(A), the transition from anharmonic to harmonic motion becomes evident.
5. An extended analysis of the time-evolution of the total energy, including dissipative effects may also be carried out