See-Saw with double pivot

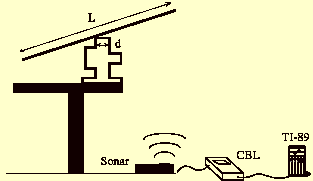
The restoring torque is due to gravity and to pivot reaction. Torque depends on the oscillation amplitude F because the effective component of the gravity force is not constant:

The lever arm of the torque is constant, and for small oscillations (and d<<L)

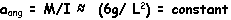
The vertical component of the acceleration of the bar ends is

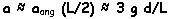
The center of mass "rebounces" like in the Galileo Oscillator.
 
 

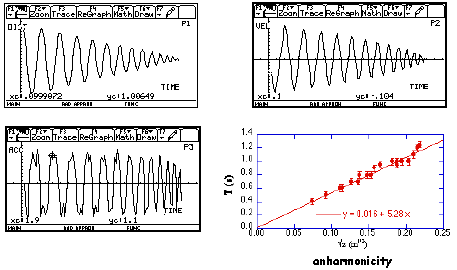
  1. The plots x(t), v(t), a(t) vs. time show the same behavior as in the Galileo Oscillator.
  2. Using the small angle approximation the predicted acceleration of the bar end is constant a=3gd/L
  3. The period T may be measured and plotted versus the square root of the oscillation amplitude z showing the agreement with the predicted slope 
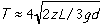
  4. By repeating the experiment with heavy masses at the bar ends (well simulating the motion of a real see-saw) it can be shown that acceleration changes into a=gd/L, 1/3 of the value measured for the unloaded bar.

 
 

See-Saw with round pivot

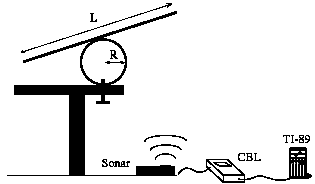
The restoring torque is due to gravity and to pivot reaction.

Torque depends on the oscillation amplitude f

The effective component of the gravity force is not constant:

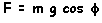
Here also the lever arm of the torque is not constant:

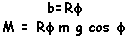
While the momentum of inertia is nearly constant:

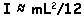
For small oscillations and d<<L

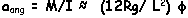
This equation is the same as the equation of a pendulum (for small oscillations) with reduced length l=L2/12R.

In the same approximation the motion is harmonic.

(The same analysis may be applied to the motion of a rocking-chair)
 
 



 
 

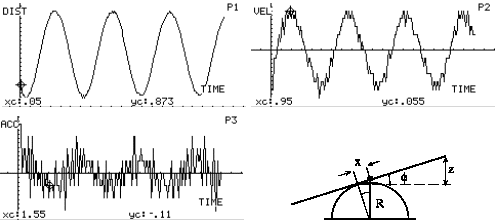
  1. The plots x(t), v(t), a(t) vs. time show a different behavior from that of the see-saw with double pivot.
  2. Now the period is independent of the amplitude: the motion here is harmonic.
  3. The teacher may guide the students to calculate the torque and the moment of inertia, suggesting suitable approximations in order to find the theoretical relationship between angular acceleration a and tilt angle f: a=—12gR/L2f: that is the classic pendulum equation.
  4. Also here the oscillation measured with a bar loaded at the ends shows an angular accelerationa=—4gR/L2f, reduced of a factor 1/3 with respect to the unloaded bar.

    5.  

     
     

    CONTINUE ...