Uno studio sperimentale del moto
lungo un piano inclinato

G. Torzo, Dipartimento di Fisica, Università di Padova

Perché uno studio del moto sul piano inclinato?
 
 

Il moto lungo un piano inclinato viene trattato in tutti i libri di testo di fisica. Tuttavia in moltissimi casi esso viene utilizzato solo come una illustrazione del modello di moto di un punto materiale, e molto spesso sotto l'azione della sola forza di gravità.

Studiare questo fenomeno sperimentalmente con metodi tradizionali significa o sterilizzare il più possibile il fenomeno "purgandolo" dalla "fastidiosa" presenza dell'attrito (rotaie a cuscino d'aria, carrelli speciali, dischi a ghiaccio secco…) oppure usare dei metodi di analisi che richiedono una elaborazione molto sofisticata e estremamente tediosa dei dati sperimentali (ad esempio ipotesi a priori sul tipo di attrito, da confrontare con dati presi in sistemi a singolo traguardo).

Nè l’una scelta nè l’altra sembra in grado di favorire la costruzione di solidi legami fra esperienza concreta e interpretazione formale, cioè di valorizzare l’esperimento per quelle che sono le sue potenzialità all’interno di un percorso di apprendimento.

Nel primo caso infatti si finisce col presentare allo studente fenomeni artificiali che poco hanno a che fare con la realtà di tutti i giorni e nei quali l’artificio contiene già tutta la fisica che si vorrebbe far apprendere agli studenti. Nel secondo caso la fisica viene schiacciata sotto un apparato di formule e un fardello di calcoli così che alla fine l'unico interessato ai risultati raggiunti resta probabilmente solo il professore…

L'uso di MBL (Microcomputer Based Laboratory) per lo studio del moto lungo il piano inclinato permette invece di introdurre un modello teorico per interpretare i dati sperimentali e discutere i limiti del modello stesso, senza dover usare particolari artifici nell'allestimento dell'apparato sperimentale, nonchè di studiare il fenomeno nella sua complessità consentendo di affrontare con relativa facilità anche quegli aspetti del fenomeno di solito trascurati (attrito, momento di inerzia delle ruote di un carrello…)
 
 

Un possibile percorso

Delineiamo di seguito molto sinteticamente una proposta di un possibile percorso sperimentale per lo studio del moto di corpi diversi lungo un piano inclinato, realizzabile mediante l’uso di un sensore di posizione (sonar) collegato ad un sistema di acquisizione on-line .

Non crediamo nei percorsi predefiniti, buoni per tutte le situazioni; sottolineiamo quindi che si tratta di un esempio poichè a partire dalla osservazione di un moto sul piano inclinato possono nacsere tanti diversi percorsi, ciascuno funzionale al contesto nel quale si costruisce, adatto agli studenti ai quali si rivolge e, perchè no, anche all’insegnante che lo propone e lo realizza assieme a loro. E’ un esempio che vuole mostrare delle possibilità e aprire la strada a tutti quelli che hanno voglia di cimentarsi con questo tipo di studio.

La proposta si articola in una serie di fasi, che corrispondono a livelli successivi di approfondimento nello studio del moto sul piano inclinato:

• Un "carrello speciale" (come quelli forniti dalla PASCO) in cui l’inerzia delle ruote è resa trascurabile si comporta come un "punto materiale" che scivola sul piano inclinato.

• Usando un altro tipo di carrello in cui l’inerzia delle ruote non è affatto trascurabile il modello di "punto materiale" non funziona più. Se le ruote sono omogenee e con geometria semplice (cilindri) si può tener conto del momento di inerzia di ciascuna ruota I=(1/2)mR2 e del rapporto tra massa rotante (Nm, nel caso di N ruote) e massa totale (M+Nm): secondo questo modello si prevede

• Una volta introdotto un modello che tiene conto anche dei moti di rotazione lo si può utilizzare per studiare il moto di altri corpi, ad esempio di cilindri o sfere, pieni o cavi, che rotolano sul piano inclinato. Il fattore di correzione x assume di volta in volta valori diversi e i dati sperimentali lo confermano.
• Un caso un po’ più complicato da analizzare è quello di sfere piene o cave che rotolano su una guida appoggiata sul piano inclinato. In questo caso il raggio di rotazione non coincide con quello della sfera e quindi il rapporto tra energia cinetica rotazionale ed energia cinetica traslazionale dipende dal rapporto tra diametro della sfera F e larghezza della guida D: il fattore di correzione può diventare sorprendentemente grande per FÅD.
• Si possono infine confrontare i risultati ottenuti con quelli relativi ad altri sistemi nei quali la caduta implica una rotazione, come lo yo-yo o il pendolo di Maxwell (Pecori &Torzo, 1998).

Nei paragrafi seguenti illustreremo in dettaglio solo la parte che riguarda il moto di un carrello (fasi 1 e 2) riportando e discutendo i dati sperimentali acquisiti.

Qui presentiamo una serie di dati acquisiti con una interfaccia PASCO-500. Informazioni su questo sistema sono reperibili in internet alla pagina http://www.elitalia.it. Prestazioni sostanzialmente equivalenti sono offerte dalla interfaccia ULI Vernier http://www.vernier.com o dallla interfaccia CBL Texas http://www.TI.com/calc/docs/cbl.htm. I primi due tipi di interfacce si collegano a PC (Macintosh o DOS/Windows) la terza alle calcolatrici grafiche Texas (TI89 o TI92…).
 

Moto di un carrello lungo un piano inclinato

Analizzando l'andamento delle variabili posizione, velocità e accelerazione nel tempo durante la salita e la successiva discesa del carrello di un carrello lungo un piano inclinato, è possibile mettere in evidenza le principali caratteristiche del moto.

Tale analisi permette infatti di

• avere informazioni sulla forza di attrito agente sul carrello dal confronto fra l'andamento delle velocità in salita e in discesa lungo il piano
• calcolare la componente dell'accelerazione dovuta alla sola gravità e confrontarla con quella attesa sulla base di una schematizzazione del carrello come punto materiale
• analizzare situazioni in cui vengono variati alcuni parametri della configurazione sperimentale (massa del corpo, attrito col piano) e controllarne l’effetto sulle variabili caratteristiche del moto
• studiare la dipendenza della componente dell'accelerazione dovuta alla gravità dalla inclinazione del piano mettendo in evidenza i limiti della schematizzazione utilizzata e l'opportunità di introdurne una che tenga conto del moto di rotazione delle ruote.

A tale scopo si possono proporre una serie di esperimenti:

1. Moto di un carrello scarico, con piccolo attrito e inerzia rotazionale trascurabile

Scopo dell’esperimento è confrontare i dati sperimentali con le previsioni formulate considerando il carrello come un punto materiale che si muove sotto l’azione della componente della forza di gravità parallela al piano. La figura 1 schematizza l'apparato sperimentale: una rotaia PASCO è appoggiata sul tavolo con un libro posto sotto una delle estremità. Il sensore di distanza è posto alla fine della rotaia dalla parte sollevata dal libro, cosicchè la distanza misurata decresce quando il carrello sale avvicinandosi al sensore, e aumenta quando il carrello scende allontanandosi dal sensore. Per lanciare il carrello si è usata una molla compressa e poi lasciata libera cosicchè il carrello ritornando in basso compie una serie di rimbalzi.

Figura 1

La figura 2 riporta i dati acquisiti utilizzando un carrello PASCO (m = 474 g) lanciato verso l’alto su un piano inclinato di 5.2 gradi sulla orizzontale .

Nelle condizioni sperimentali in cui si è effettuata questa misura, l’accelerazione prevista vale
a = g.sina = (0.89 ±0.02)m/s2, assumendo una incertezza sulla inclinazione di 0.1 gradi.

Per controllare la validità della schematizzazione in termini di punto materiale si può ricavare dai dati sperimentali il valore dell’accelerazione del carrello e confrontarlo con quello previsto.

A tale scopo è necessario analizzare in dettaglio il grafico v(t), isolando una porzione di grafico corrispondente ad una salita e discesa del carrello (tratto approssimativamente rettilineo con pendenza positiva) e ricavando la pendenza della corrispondente retta di interpolazione (Fig. 2).

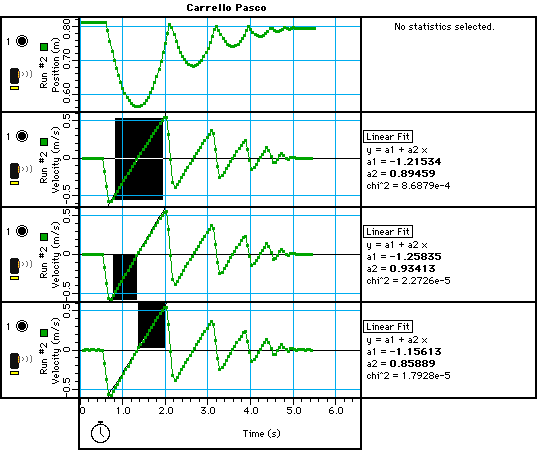
Figura 2

Il valore ottenuto per l’accelerazione, a =(0.895±0.005) m/s², è in ottimo accordo con la previsione, a = (0.89±0.02) m/s² , tuttavia una analisi più fine del grafico v(t) mette in evidenza che l’accelerazione misurata non ha lo stesso valore in salita e in discesa (figura 2, grafici 3 e 4).

Selezionando le due diverse porzioni del grafico si ottengono due rette di interpolazione rispettivamente con coefficienti:

Salita a_s = (0.934±0.005) m/s²

Discesa a_d = (0.859±0.005) m/s²

La differenza fra i due valori è dovuta alla presenza di una forza di attrito che agendo sempre in direzione opposta alla velocità del carrello si somma in salita e si sottrae in discesa alla componente della forza di gravità.

Facendo una media fra le due accelerazioni si ottiene un valore che corrisponde alla componente dovuta alla sola gravità:

a_m= (a_s + a_d)/2 = (a_g + a_att + a_g – a_att)/2 = (0.90±0.01) m/s²

Questo valore di accelerazione è concettualmente più corretto di quello che si ottiene dalla interpolazione unica dei dati di salita e discesa. Infatti interpolando separatamente i due tratti e facendo successivamente la media dei valori ottenuti si dà uguale peso ai due valori di accelerazione indipendentemente dal numero dei punti acquisiti in salita e in discesa.

Una stima del valore della accelerazione dovuta all’attrito si ricava dalla semidifferenza dei due valori di accelerazione trovati. Nel nostro caso:

a_att = (a_s – a_d)/2 =(0.04±0.01) m/s² , e quindi, tenendo conto che la massa del carrello è M=0.474 kg, la forza di attrito misurata è F_att =Ma_att = 0.02 N.
 

Considerazioni didattiche

Il passaggio dal fenomeno reale alla schematizzazione in termini di moto di un punto materiale è un passaggio concettualmente molto importante e didatticamente delicato.

Pertanto è importante che, prima di passare all’acquisizione dei dati e alla visualizzazione dei grafici, gli studenti abbiano modo di osservare con cura l’andamento del fenomeno e di formulare previsioni sull’andamento della posizione, velocità e accelerazione in funzione del tempo. Questa operazione permette, in primo luogo, di stabilire criteri per decidere se l’acquisizione può essere considerata "buona", cioè per scartare quelle eventualmente disturbate da eventi estranei al fenomeno studiato (ad esempio l’interferenza sul segnale raccolto dal sonar dovuta alla presenza di una parete riflettente diversa dal carrello). In secondo luogo, la formulazione a priori di ipotesi sulla forma dei grafici permette poi di confrontare le previsioni degli studenti con i risultati sperimentali e di avviare quindi una discussione sullo schema teorico utilizzato nel formulare tali previsioni.

Nell’esempio di analisi riportato, per ricavare i valori dell’accelerazione, si è utilizzato il fit sui dati di velocità che presenta il vantaggio di lavorare su un grafico nel quale sono facilmente identificabili le porzioni del moto da selezionare. Tuttavia sarebbe opportuno effettuare anche interpolazioni sul grafico della posizione in funzione del tempo, che danno ovviamente risultati confrontabili, per avere la possibilità di discutere con gli studenti il significato dei parametri ottenuti nei due casi. Un esempio di analisi è riportato in figura 3.

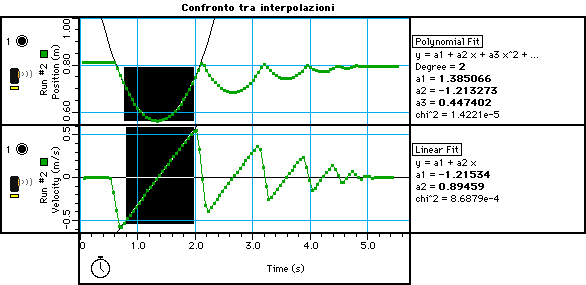
Figura 3

Nell’analisi riportata come esempio non sono stati utilizzati i dati relativi ai rimbalzi del carrello; in realtà essi potrebbero venire analizzati per sottolineare l’indipendenza del valore della accelerazione dalla velocità iniziale e dalla lunghezza del percorso. Infatti una analisi del moto dopo il rimbalzo, condotta analogamente a quella sopra riportata, permette di vedere che il moto del carrello in salita e in discesa presenta ancora le stesse caratteristiche (stessa forma dei grafici, stessa accelerazione) con la sola differenza del valore della velocità iniziale e quindi della distanza percorsa prima e dopo l’inversione del moto.

Inoltre la selezione dei dati dai quali ricavare il valore dell’accelerazione potrebbe costituire una buona occasione per distinguere le diverse fasi del moto, identificando oltre alla fase in esame (salita e discesa) quella di interazione con il respingente a molla, che potrebbe essere oggetto di uno studio successivo.

Questo esperimento, come quelli che seguono, si presta tanto ad una esecuzione collettiva, sfruttando la possibilità di passare ai diversi gruppi i dati raccolti, sia ad una esecuzione a gruppi e ad un successivo confronto dei dati raccolti dai diversi gruppi. La prima alternativa potrebbe essere più indicata se gli studenti non hanno ancora una sufficiente confidenza con l'apparato sperimentale, in quanto permette poi di effettuare tutti insieme una elaborazione "guidata" dei dati acquisiti. La seconda alternativa risulta invece particolarmente efficace quando gli studenti sono in grado di condurre autonomamente l’esperimento e fornisce certamente un panorama più ricco di dati su cui discutere con tutta la classe.
 

b) Moto di un carrello caricato con una massa aggiuntiva

Scopo dell’esperimento è mettere in evidenza che, come previsto dal modello teorico utilizzato per interpretare i dati sperimentali ricavati nell’esperimento descritto al punto a), un aumento della massa del carrello non ha effetto sulla componente della accelerazione dovuta alla gravità.

Caricando il carrello con una massa aggiuntiva di 500 grammi si sono ottenuti i risultati riportati in figura 4.

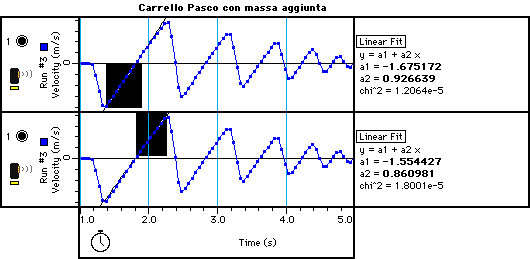
Figura 4

Come si può vedere il valore dell’accelerazione dovuta alla gravità rimane invariato,
a =(0.90±0.01) m/s², come pure quella dovuta all’attrito a_att = (0.03±0.01) m/s².
 

c) Moto di un carrello con maggiore attrito

Scopo dell’esperimento è controllare che la differenza tra il valore dell’accelerazione in salita e quello in discesa è effettivamente riconducibile alla presenza di una forza di attrito.

Si può ripetere l’esperimento descritto al punto a) aumentando volutamente l’attrito. Incollando sul fondo del carrello un pezzetto di spugna che striscia contro il piano, ad esempio, si sono ottenuti i risultati riportati in figura 5.

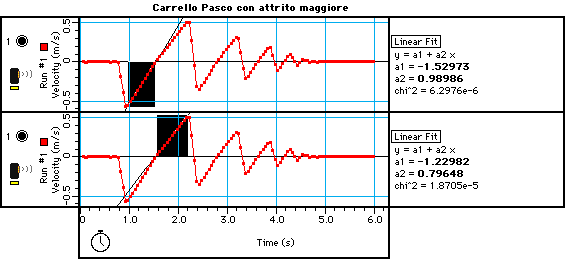
Figura 5

In questo caso il valore della accelerazione dovuta alla gravità è ancora sostanzialmente invariato
a =(0.89±0.01) m/s², mentre quello dell’accelerazione dovuta all’attrito è notevolmente più grande a_att = (0.10±0.0)1 m/s², come è immediatamente evidente dal confronto delle due pendenze nei grafici.

In questo esperimento il coefficiente di attrito risulta circa 3 volte quello dell'esperimento precedente.
 
 

d) Moto di un carrello con inerzia rotazionale non trascurabile

Scopo dell’esperimento è mettere in evidenza che vi sono casi in cui la schematizzazione del moto di un carrello in termini di moto di un punto materiale non è adeguata, in quanto non permette di rendere conto dei dati sperimentali.

I dati che riportiamo in figura 6 sono stati ottenuti con un carrello in alluminio con 3 ruote cilindriche il cui momento di inerzia è facilmente calcolabile I=(1/2)mR2.

In questo caso il valore medio delle due pendenze a=(0.82±0.01) m/s² è minore di quello previsto sulla base di un modello che schematizza il carrello come punto materiale (0.89±0.02) m/s².

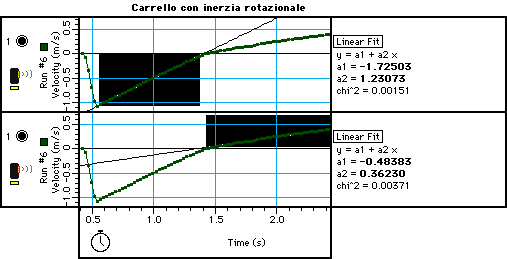
Figura 6

Poichè l’unica variazione introdotta rispetto alla serie precedente di esperimenti è il tipo di carrello utilizzato, dotato nel secondo caso di ruote più pesanti, si può formulare l’ipotesi che in questo caso, a differenza dei precedenti, il moto di rotazione delle ruote costituisca un dettaglio del fenomeno non trascurabile.

Per controllare questa ipotesi è necessario rivedere il modello teorico utilizzato per prevedere l’accelerazione del carrello. Se si tiene conto del moto di rotazione delle ruote, l’espressione della accelerazione diviene (vedi "considerazioni didattiche" più avanti):

a = gsina/(1 + I/MR²)

dove M è la massa totale del carrello, I il momento di inerzia totale delle ruote, R il raggio delle ruote.

Assumendo che ciascuna ruota (di massa m) possa essere considerata un cilindro di momento di inerzia I = mR²/2 si ottiene per l'accelerazione:

a = gsina/(1 + 3m/2M)

che mostra come la correzione rispetto al valore gsina dipende solo dal rapporto m/M. Ciò significa che la differenza tra i due valori teorici dell’accelerazione, senza e con rotazione, dipende anch’essa dal rapporto fra le masse ed è proporzionale a sina. Ripetendo la misura con diversi valori della inclinazione si può tracciare un grafico di a in funzione di sina.

In figura 7 è tracciata la retta (tratto continuo) con pendenza g e quella con pendenza g/(1+3m/2M) (tratteggiata), calcolata con i valori misurati M=678 g, m=46.

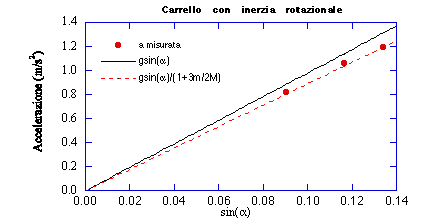
Figura 7

Il confronto con le rette corrispondenti ai due modelli teorici considerati mostra che i dati sperimentali sono meglio rappresentati dal modello che tiene conto del moto di rotazione delle ruote.

Considerazioni didattiche

Ci sembra consigliabile, dal punto di vista didattico, non basarsi su di un solo esperimento per introdurre la revisione del modello teorico.

Suggeriamo quindi di proporre uno studio del moto del carrello in funzione della pendenza del piano, alla ricerca di eventuali regolarità che forniscano una più solida base sperimentale per l’operazione di revisione.

Si tratta infatti di mettere in evidenza che l’effetto riscontrato in questo esperimento si ripropone, al variare dell’inclinazione, con caratteristiche di regolarità: agisce sempre nella stessa direzione (producendo una accelerazione minore di quella prevista) e la differenza fra il valore previsto e quello sperimentale aumenta all’aumentare del valore dell’accelerazione.

Per quanto riguarda il calcolo del fattore di correzione sul valore teorico previsto per l’accelerazione la via più semplice, e anche più facile da giustificare intuitivamente, è quella del bilancio energetico.

Infatti, anche se gli studenti non hanno molta confidenza con lo studio dei moti di rotazione, non è difficile riconoscere la presenza di un’altra forma di energia legata al moto delle ruote oltre alla energia cinetica legata al moto di traslazione del carrello.

L’energia totale del sistema coincide con l’energia potenziale del carrello quando questo si trova istantaneamente fermo nella posizione più elevata sul piano inclinato. Se fissiamo lo zero della energia potenziale a livello del tavolo orizzontale su cui poggia il piano (o meglio a livello della posizione del baricentro del carrello quando tocca il respingente), quando il carrello raggiunge tale livello l’energia totale sarà uguale alla somma di una componente di energia cinetica dovuta al moto di traslazione del carrello nel suo complesso e di una dovuta al moto di rotazione delle ruote.

Mgh = Mv²/2 + Iw ²/2

(M è la massa del carrello, h il dislivello rispetto al riferimento fissato per l’energia potenziale, v la velocità finale del carrello, I il momento di inerzia totale delle ruote, w la velocità angolare finale delle ruote)

Se possiamo supporre che le ruote girino senza mai strisciare sul piano, possiamo esprimere la velocità angolare come w = v/R, con R raggio della ruota; inoltre possiamo sostituire al momento di inerzia totale la somma dei momenti di inerzia di tre dischi dello stesso raggio, ottenendo così:

Mgh = Mv²/2 + 3mv²/2 = Mv²(1 + 3m/2M)

Da cui possiamo ricavare l’espressione della velocità finale

che confrontata con quella che otterremmo in assenza di rotazione (m = 0) ci indica che in questo caso l’accelerazione è ridotta di un fattore k = 1/(1 + 3m/2M).

Pertanto, poichè quella che misuriamo è la componente dell’accelerazione parallela al piano, il nuovo modello prevede per l’accelerazione del carrello:

a = gsina/(1 + 3m/2M)

Il ruolo di questo esperimento è quello di introdurre gli studenti allo studio di moto reali, per i quali molto spesso la schematizzazione in termini di punto materiale risulta inadeguata.

Se non si ritiene opportuno introdurre la trattazione analitica che porta alla nuova espressione dell’accelerazione (perchè, per esempio, non si sono trattati in precedenza i moti rotatori e i momenti di inerzia), si può limitare l’elaborazione dei dati alla costruzione del grafico di a_m in funzione di sina. Una discussione qualitativa dei dati sperimentali, infatti, può mettere in evidenza che il carrello si comporta come se avesse una inerzia maggiore di M: a parità di energia totale a disposizione del sistema, il carrello raggiunge una velocità finale inferiore a quella prevista v=Ã(2gh) e quindi anche il valore sperimentale dell’accelerazione risulterà inferiore a quello previsto. Queste considerazioni sono sufficienti per mettere in evidenza l’inadeguatezza del modello fino a quel punto considerato.

La trattazione analitica dettagliata è invece necessaria se si vuole che questi esperimenti costituiscano il punto di partenza di uno studio dei moti di rototraslazione, in particolare dello studio del moto di corpi che rotolano lungo un piano inclinato, così come previsto nell’esempio di percorso delineato precedentemente.
 
 

Perché utilizzare MBL?

La possibilità di condurre uno studio sperimentale del tipo di quello qui esemplificato è legata alla disponibilità di sistemi di acquisizione on-line basati sull’interfacciamento di sensori con un computer. Il Microcomputer Based Laboratory infatti consente:

Queste caratteristiche consentono un risparmio di tempo nella raccolta ed elaborazione dei dati, facilitano il confronto fra i risultati di esperimenti in cui vengono fatti variare alcuni parametri signifcativi, rendono cioè disponibile una grande varietà di dati e immediatamente visualizzabili le loro interrelazioni consentendo di cogliere regolarità o inconsistenze e quindi di attribuire significato fisico alla modellizzazione matematica.

Più in generale, si può dire che le caratteristiche di un sistema di acquisizione on-line rendono possibile proporre percorsi didattici per lo studio sperimentale di un fenomeno fisico strutturati su diversi piani, sintetizzabili nel seguente ciclo:

• Ripresa del ciclo.

Pensiamo che in questo modo lo studente possa essere introdotto all'uso consapevole degli strumenti di indagine tipici della fisica e che indagini di questo tipo possano fornire un esempio della soddisfazione intellettuale legata al capire "come vanno le cose" che è componente essenziale del gusto che la fisica può dare.
 
 

Riferimenti