
FIGURE 1. Position and velocity vs. time of a bouncing ping-pong ball.
Barbara Pecori, Physics Department, University of Bologna (Italy)
Giacomo Torzo, Physics Department, University of Padova (Italy)
Low cost interfaces and sensors offer new possibilities to hands-on physics education by making on-line investigations easy and accessible to secondary school pupils. The educational potential of the system is highly enhanced by the related software that allows quick and flexible data handling.
We here illustrate a path for investigating the motion of falling objects in order to show that on-line acquisition systems can stimulate the curiosity of understanding how ordinary life things work.
The path we selected is particularly suited to give an example of the interplay between collection and interpretation of experimental data peculiar of scientific investigation of phenomena: the first level theoretical model (point mass) is adapted in order to account for experimental data and viceversa the experimental set up is modified in order to check the validity of the new model (rigid body).
All data have been collected by using a ULI-Vernier interface (the software DataLogger may be downloaded for Macintosh at http://www.vernier.com/tech/HRM.sea.hqx or for DOS at http://www.vernier.com/tech/doshrm.zip), and they may be seen as text files (5 files in ASCII format as: pingpong.txt, yoyo.txt, pinball.txt, maxwell.txt, yoyospec.txt. Data are listed in 3 columns: time, position, velocity. Position is given as distance from the surface below. See also reference (1) and the file ReadMe.
We start by investigating the motion of a ping-pong ball bouncing on the floor (see figure 1).

FIGURE 1. Position and velocity vs. time of a bouncing ping-pong ball.
The software allows us to obtain the graphs of the position and velocity versus time and to calculate the acceleration during the rise and fall of the body by interpolating the experimental data.
The calculated value shows that the model of a point mass moving in a constant acceleration field of intensity g accounts well enough for the collected data.
We can now compare the motion of the ball with that of another object: the yo-yo (see figure 2).
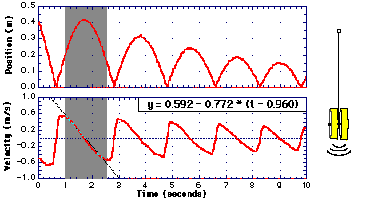
FIGURE 2. Position and velocity vs. time of a yo-yo.
The yo-yo falls much slower than the ping-pong ball and this can be easily connected to the fact that, unlike the ball, it must rotate in order to fall.
To account for the smaller acceleration we need to adopt a model that also considers the rotational motion of the yo-yo.
The easiest way is to derive the expression of the velocity of the center
of mass from the energy balance, thus obtaining ![]() that,
compared with the corresponding equation for a free falling body, suggests
that the Yo-yo is falling with the acceleration
that,
compared with the corresponding equation for a free falling body, suggests
that the Yo-yo is falling with the acceleration
a=g / (1+I/mr2)
This is not easily checked with experimental data because the moment of inertia of the yo-yo can be only roughly estimated.
In order to check the model we need to analyze the motion of a similar object whose moment of inertia can be easily calculated. We shall look at the motion of a "pinned ball" (see figure 3).
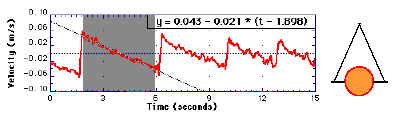
FIGURE 3. Velocity vs. time of a pinned ball.
In the case of a sphere we have 1+I/mr2 =1+(2/5)(R/r)2 = k and the theoretical value of the acceleration (with R=18.5 mm, r=0.4 mm) is
a = g/k = 0.011 m/s2
which is of the expected order of magnitude but clearly underestimated if compared with the experimental value of a =0.021 m/s2.
We have neglected some feature of the system that makes the acceleration much bigger than expected... for example something that makes the system to behave as if the axis radius were bigger.
Can the string thickness have such an effect?
The measured value of string diameter is d=0.3mm that gives an effective
axis radius
r' = r+d/2 = 0.55 mm and a calculated acceleration
a = 0.022 m/s2
We expect the wire thickness to become negligible for greater values of the axis radius.
To check this we can use a more sophisticated object called the Maxwell wheel (see figure 4).
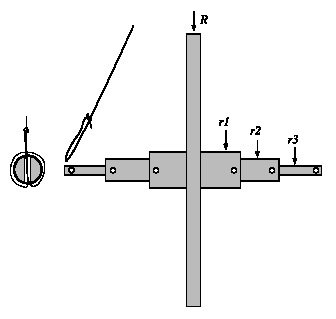
FIGURE 4. Triple axis Maxwell wheel.
In this case, taking into account that the axis has negligible momentum of inertia, but non-negligible mass, we have k=1+[(m-ma)/(2m)](R/r)2
A comparison of the measured and calculated values of a for two different values of the axis radius shows how the effect of the string decreases as the axis radius increases (see table 1).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TABLE 1. Effect of the string on two different axis values of the Maxwell wheel.
We can now use all the results obtained to explain the motion of the yo-yo in detail.
A closer look at the velocity graph of the yo-yo shows that the acceleration is not constant during its upward-downward motion: it is greater in the higher positions (where the wire is wound up) and smaller in the lower positions (where the wire is unwound).
We can interpret the differences in the value of the acceleration as differences in the effective radius of the axis due to the wire wounding on itself.
We can finally check our interpretation by analyzing the motion of a special yo-yo (see figure 5) where the axis radius is intentionally made variable by gluing two plastic cones to a glass sphere.
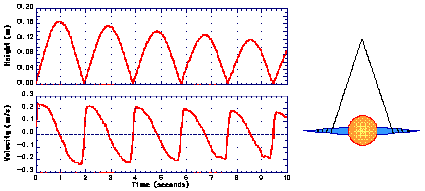
FIGURE 5. Position and velocity vs. time of a special yo-yo.
The comparison of the velocity graph with the one we had for the yo-yo confirms our interpretation of the experimental data.
Final Remarks
We illustrated a possible path for investigating the motion of falling bodies which starts from the study of the motion of a body that can be interpreted with a point mass model, then focus on the necessity to revise the model when the falling body also rotates. The new model is then made more and more sophisticated in order to account for the experimental data, by devising new shapes of the falling body that allow us to check the ipotheses put forward in order to explain the motion of the original object.
The path illustrated here has been constructed for the purpose of this contribution and it is not necessarily the optimal path to put forward to the students, which will depend on the teaching context. It was designed to give an example of how teachers can exploit the potentialities of an on line acquisition system in the school laboratory, focussing mainly on the possibility it offers to investigate ordinary life phenomena from the point of view of physics and to help the students to become acquainted with the cognitive tools peculiar to physics knowledge, by fostering the recognition of common patterns in phenomena that look different and facilitating the process of gradual refinement of the theoretical model that can account for experimental data.
We believe that this kind of investigation can give the students an example of the intellectual satisfaction of explaining how things work which is a basic component of the "fun" one can get from physics.
CNR and MURST funds have supported the research.